reading-notes
Graphs
A graph is a non-linear data structure that can be looked at as a collection of vertices (or nodes) potentially connected by line segments named edges.
Directed vs Undirected
Undirected Graphs
An Undirected Graph is a graph where each edge is undirected or bi-directional. This means that the undirected graph does not move in any direction.
For example, in the graph below, Node C is connected to Node A, Node E and Node B. There are no “directions” given to point to specific vertices. The connection is bi-directional.
Directed Graphs (Digraph)
A Directed Graph also called a Digraph is a graph where every edge is directed.
Unlike an undirected graph, a Digraph has direction. Each node is directed at another node with a specific requirement of what node should be referenced next.
Compare the visual below with the undirected graph above. Can you see the difference? The Digraph has arrows pointing to specific nodes.
Complete vs Connected vs Disconnected
There are many different types of graphs. This depends on how connected the graphs are to other node/vertices.
Complete Graphs
A complete graph is when all nodes are connected to all other nodes.
Connected
A connected graph is graph that has all of vertices/nodes have at least one edge.
Disconnected
A disconnected graph is a graph where some vertices may not have edges.
Acyclic vs Cyclic
Acyclic Graph
An acyclic graph is a directed graph without cycles.
A cycle is when a node can be traversed through and potentially end up back at itself.
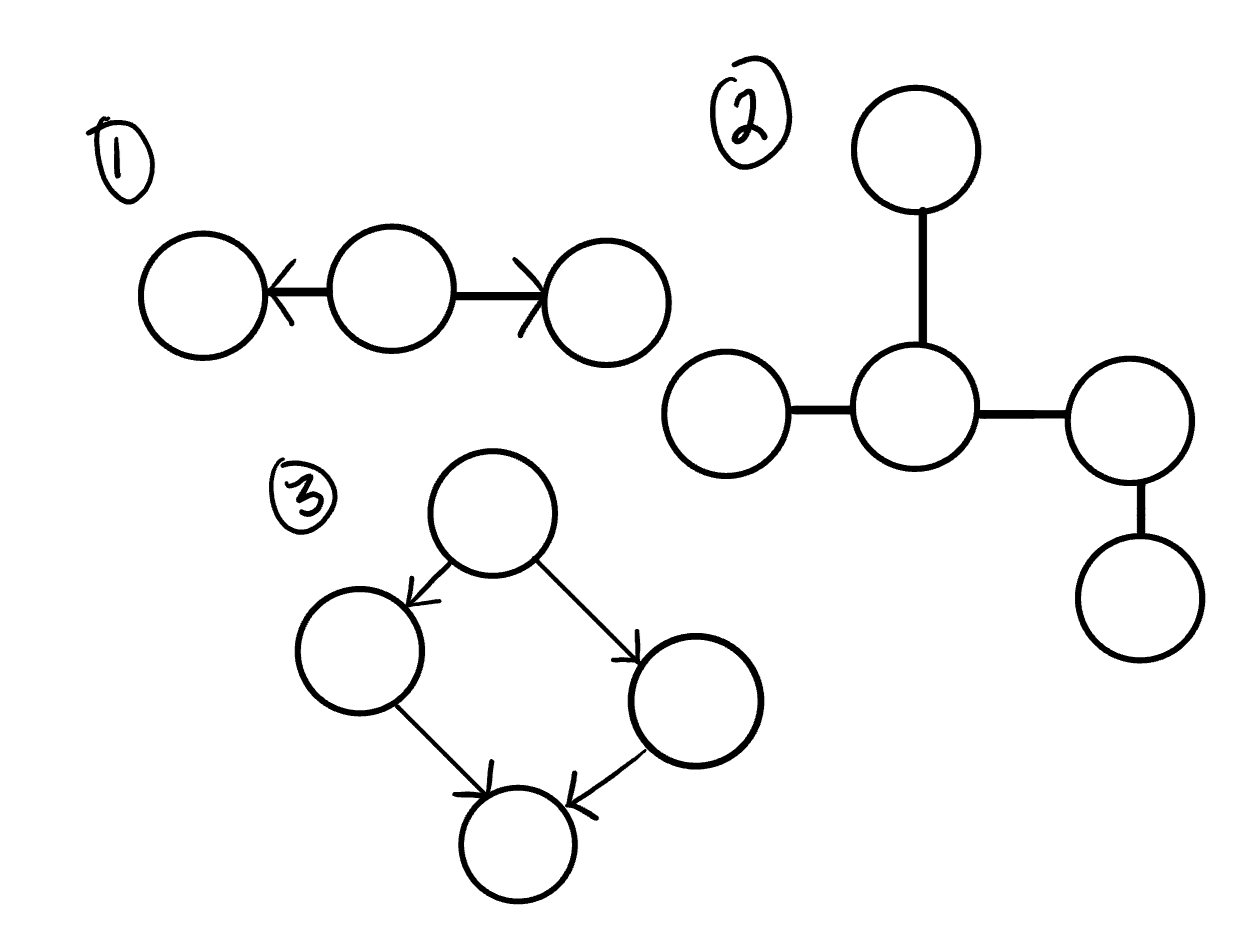
Cyclic Graphs
A Cyclic graph is a graph that has cycles.
A cycle is defined as a path of a positive length that starts and ends at the same vertex.
Graph Representation
We represent graphs through:
1.Adjacency Matrix
2.Adjacency List
Adjacency Matrix
An Adjacency matrix is represented through a 2-dimensional array. If there are n vertices, then we are looking at an n x n Boolean matrix
Adjacency List
An adjacency list is the most common way to represent graphs.
An adjacency list is a collection of linked lists or array that lists all of the other vertices that are connected.
Weighted Graphs
A weighted graph is a graph with numbers assigned to its edges. These numbers are called weights. This is what a weighted graph looks like:
Traversals
Breadth First
In a breadth first traversal, you are starting at a specific vertex/node. This node must be specified when calling the BreadthFirst() method. The breadth first traversal of a graph is like that of a tree, with the exception that graphs can have cycles. Traversing a graph that has cycles will result in an infinite loop….this is bad. To prevent such behavior, we need to have some way to keep track of whether a vertex has been “visited” before. Upon each visit, we’ll add the previously-unvisited vertex to a visited set, so we know not to visit it again as traversal continues.
Depth First
In a depth first traversal, our approach is a bit different than the approach used for breadth first. While the breadth first traversal uses a Queue to visit all children at a given level, the depth first traversal uses a Stack to visit all children of a given subtree. (This differs from our approach to tree traversal, where we visit nodes via recursive calls. Recursive calls use a call stack internally.)
Real World Uses of Graphs
Graphs are extremely popular when it comes to it’s uses. Here are just a few examples of graphs in use:
-
GPS and Mapping
-
Driving Directions
-
Social Networks
-
Airline Traffic
-
Netflix uses graphs for suggestions of products